Introduction

Self-avoiding walks

A self-avoiding walk (SAW) $\omega$ is a sequence of lattice vertices $(\omega_0, \omega_1, \dots, \omega_n)$ such that $\omega_i \neq \omega_j$ for $i\neq j$, and $\omega_i,\omega_{i+1}$ are adjacent on the lattice for each $i=0,\dots,n-1$. We say $\omega$ has size $|\omega| = n$.

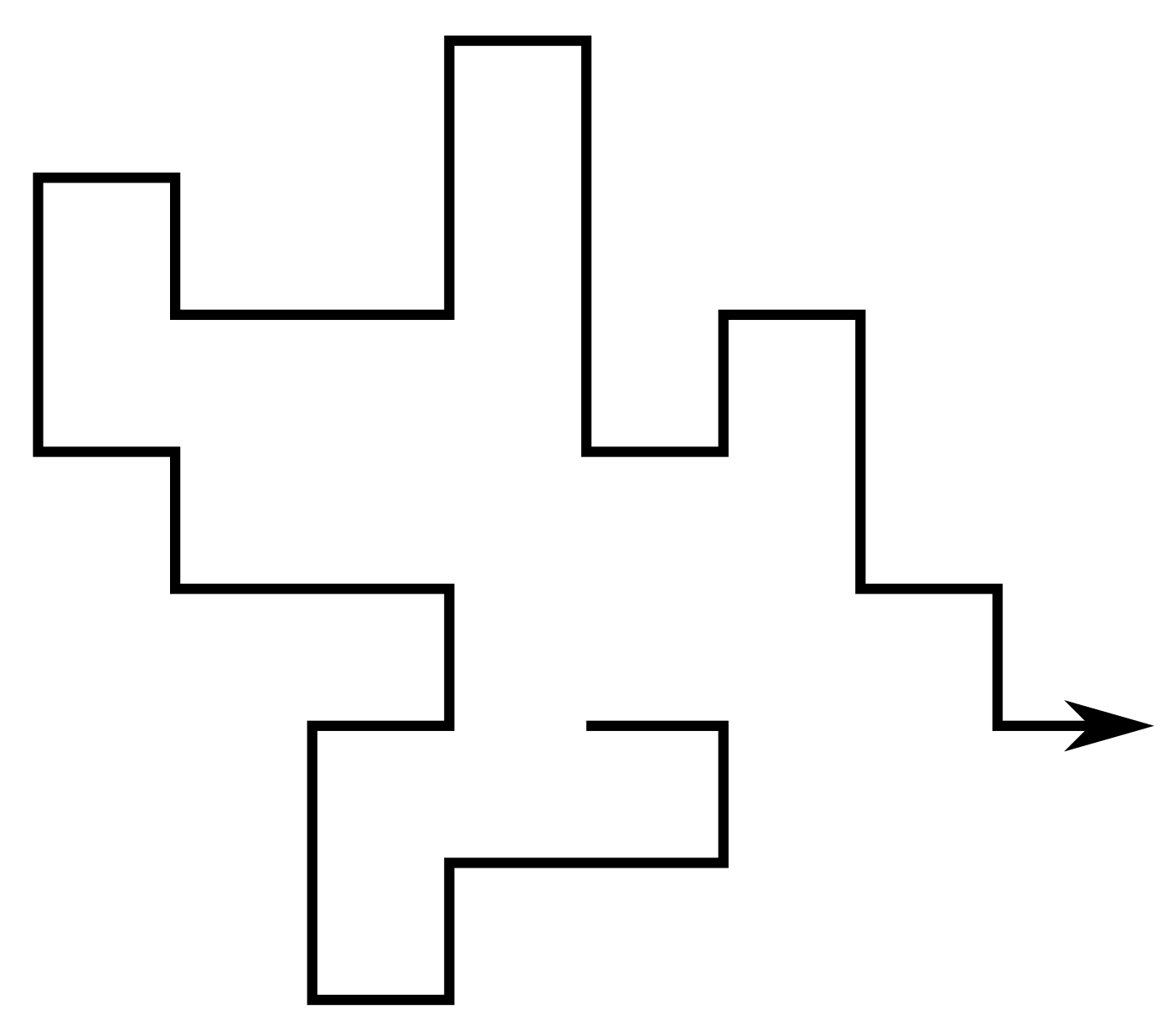Since the lattice is vertex-transitive, if one SAW is a translation of another we consider them to be the same. Equivalently assume $\omega_0 = 0$.

For a given lattice take $c_n$ to be the number of SAWs of size $n$. Then e.g. on the square lattice \[ (c_n)_{n\geq0} = (1, 4, 12, 36, 100, 284, 780, \dots) \]

Self-avoiding polygons

A self-avoiding polygon (SAP) $\pi$ is a sequence of lattice vertices $(\pi_1, \pi_1, \dots, \pi_{n})$ such that $\pi_i \neq \pi_j$ for $i\neq j$, and $\pi_i,\pi_{i+1}$ are adjacent on the lattice, and so too are $\pi_1,\pi_n$. The size of $\pi$ is $n$.

Equivalently a SAP is a SAW which ends adjacent to its initial vertex.

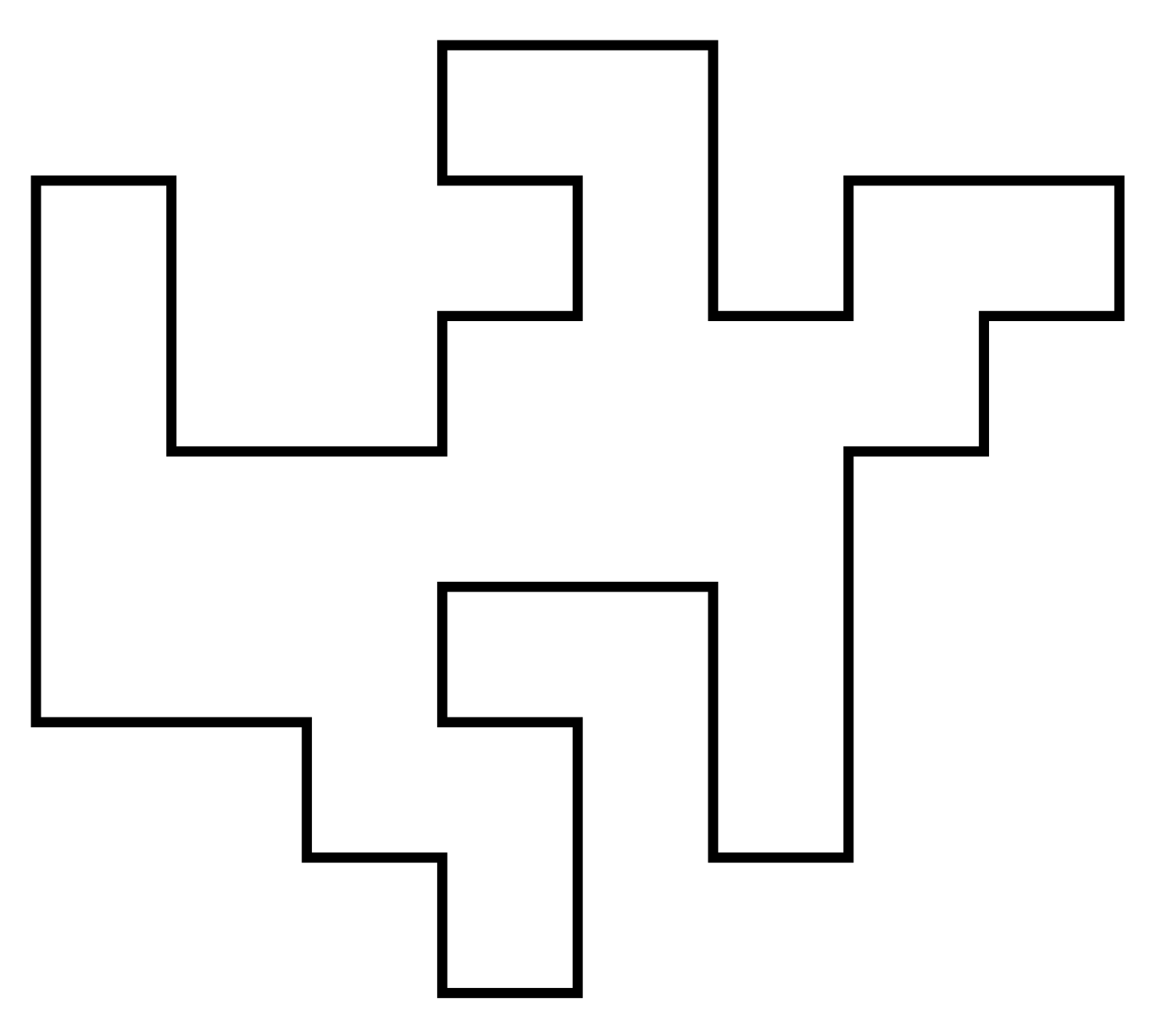
For our purposes two SAPs are the same if they are translates of one another. So there are $2n$ SAWs (of length $n-1$) corresponding to each SAP of size $n$. Let $p_n$ be the number of size-$n$ SAPs. Then e.g. on the square lattice \[ (p_n)_{n\geq4} = (1,0,2,0,7,0,28,0,124,\dots) \] (On the triangular and fcc lattices SAPs can have odd size.)

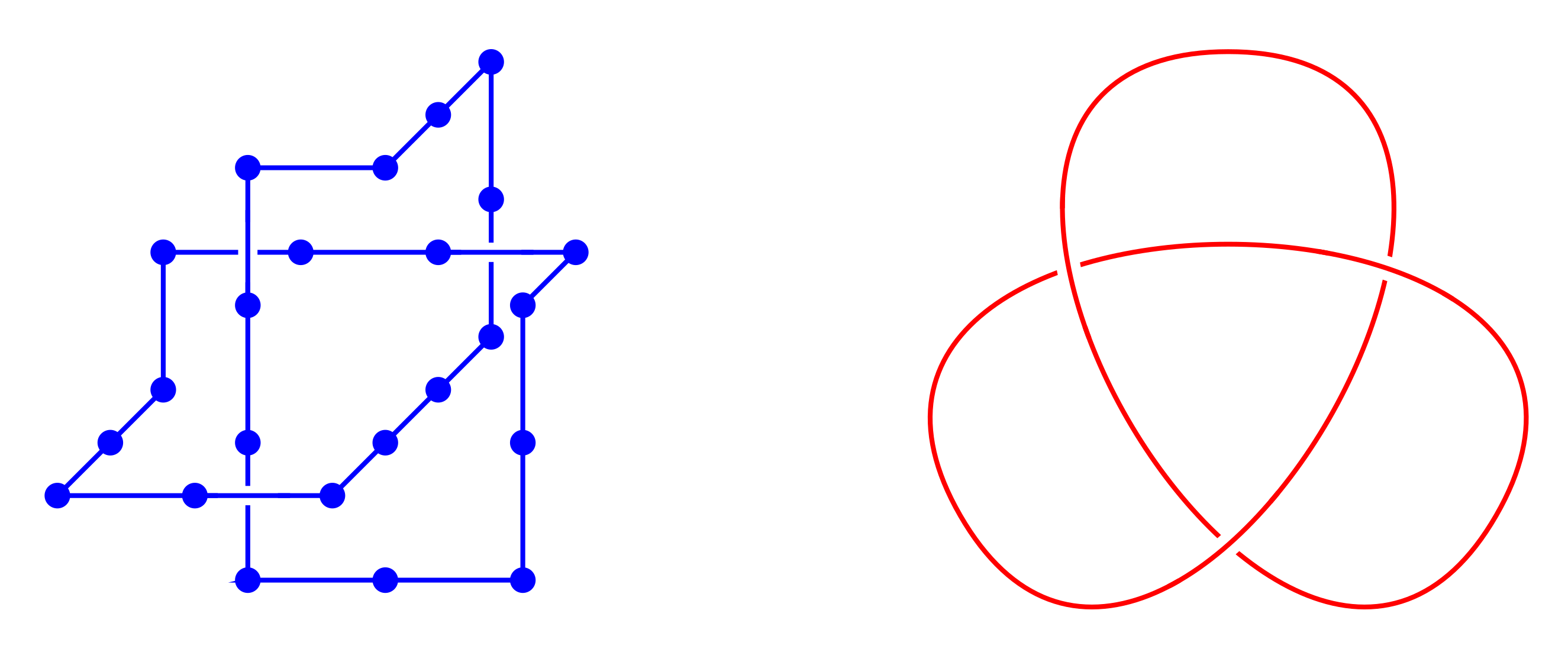
Thetas and tadpoles

SAPS have all vertices of degree 2 while SAWs have two vertices of degree 1. Here we introduce vertices of degree 3: thetas (two vertices of degree 3) and tadpoles (one degree 1 and one degree 3).

Again counted up to translation. On the square lattice \begin{align*} (\theta_n)_{n \geq 7} &= (2, 0, 12, 6, 62, 60, 338, 430, 1966, \dots) \\ (\varphi_n)_{n \geq 5} &= (8, 24, 84, 244, 740, 2072, 6004, \dots) \end{align*}

Lattices

On the square and cubic lattices, the three "arms" of a theta must have the same parity $\rightarrow$ strong parity effects. Not a problem on the triangular or fcc lattices.

Motivation

Polymer models

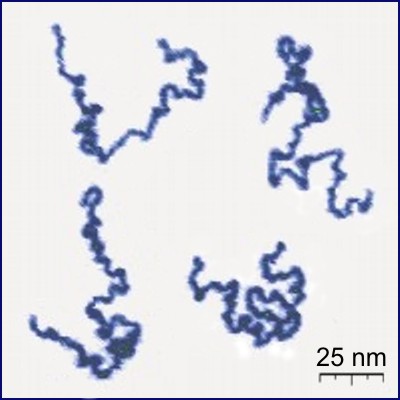
Conception for SAWs is usually credited to Paul Flory (J. Chem Phys. 1949). He was interested in a theoretical model for long linear polymer chains in solution. In particular he wanted a model which accounted for the excluded volume principle: the idea that two monomers in a chain cannot occupy the same space.

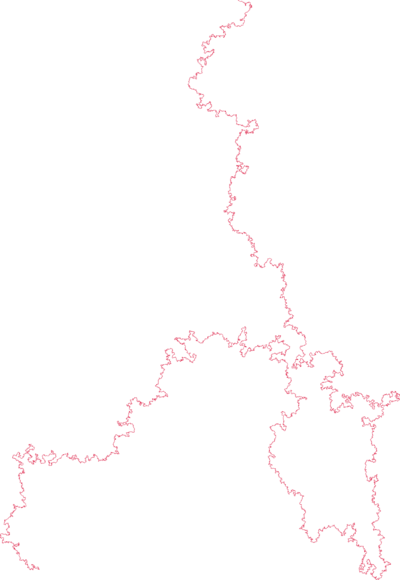poly(2-vinylpyridine) (Y. Roiter & S. Minko, J. Amer. Chem. Soc. 2005)	square lattice SAW of length $2^{25}$ (N. Clisby 201?)

SAWs (or SAPs, trees, etc., depending on the model) turn out to be a good model for polymers in a good solvent (at least for long ones).

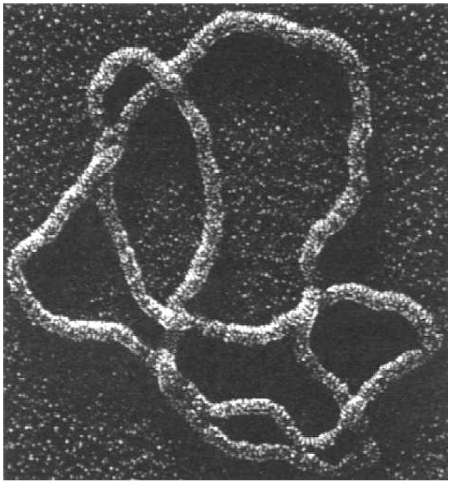
Knots

Headphone cables, shoelaces, necklaces, and even polymer molecules can get tangled up in knots and links.

H.L. Frisch and E. Wasserman (J. Amer. Chem. Soc. 1961) and M. Delbruck (Proc. Symp. Appl. Math. 1962) conjectured that random simple closed curves in $\mathbb{R}^3$ will be knotted with high probability. More precisely, the probability of being unknotted decays exponentially with the length of the curve.

	(S.A. Wasserman et al, Science 1985)

The FWD conjecture was first proved by D.W. Sumners and S.G. Whittington (J. Phys. A: Math. Gen. 1988) for SAPs on the cubic lattice. Their method used pattern theorems.

Subsequently proved for a number of other models (on and off the lattice).

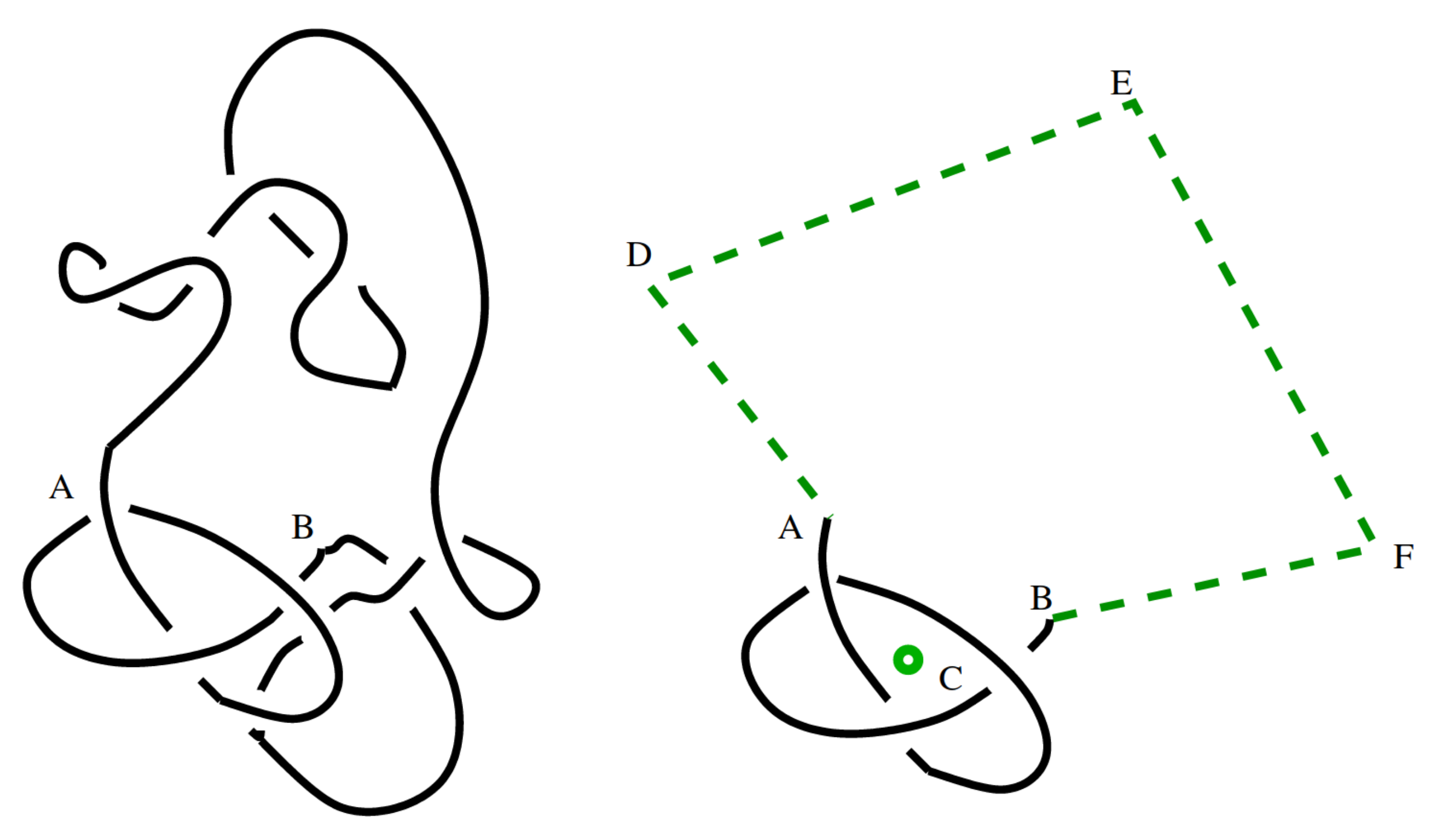
The size of knots

Knots are very likely because small "knotted parts" can be inserted into a polygon and force it to be knotted. But in turn the "knotted part" of a typical large knotted polygon is relatively small.

Different ways to estimate the "size" of the knotted part. Marcone et al (J. Phys. A 2005) use two different methods:

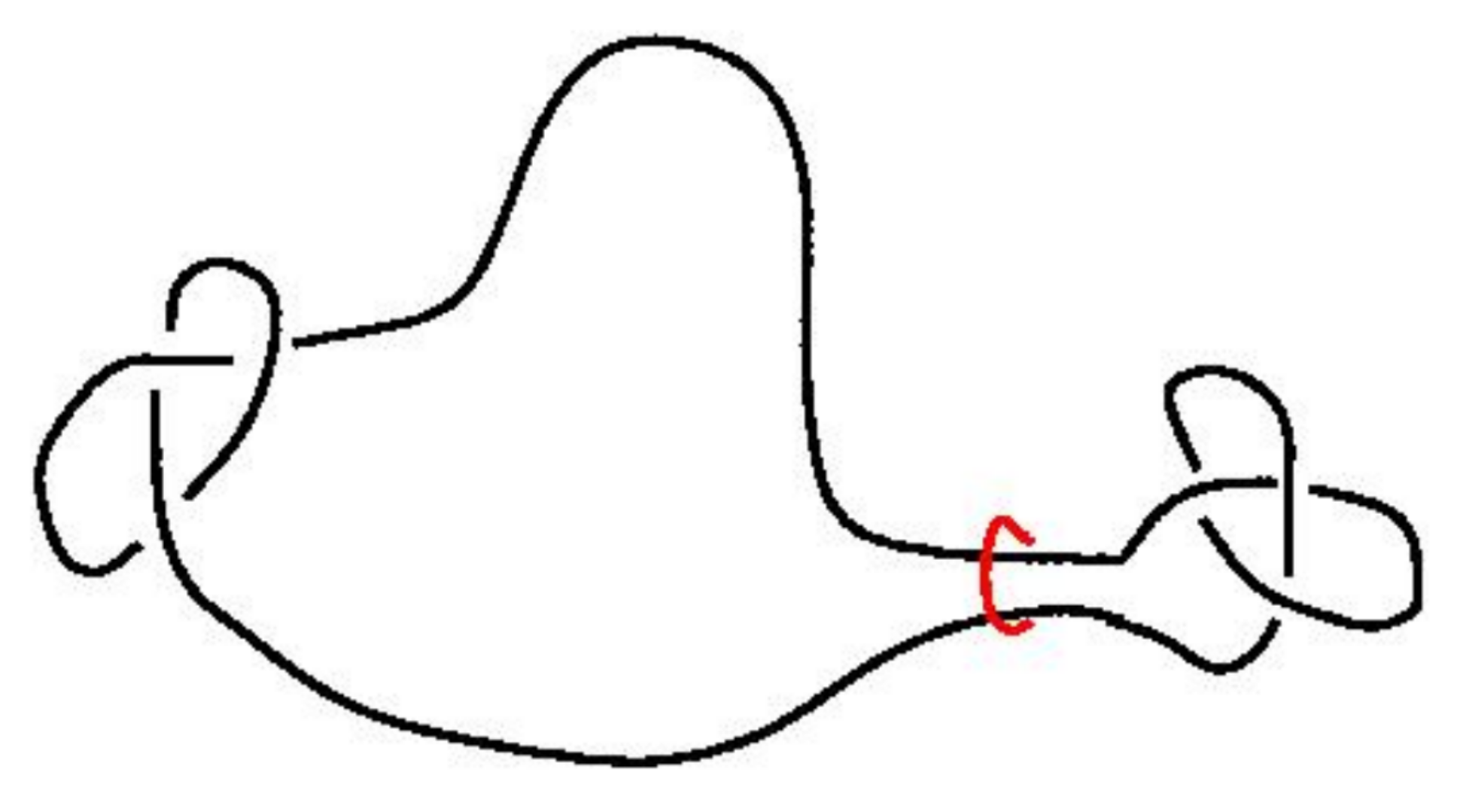Both methods lead to an estimate of the knotted part of an $n$-edge prime knot occupying $\approx n^{0.75}$ edges.

Knots vs. thetas

Question: How do the different parts of a typical theta scale in size? Most likely two arms are small and one big:

R-loops

During DNA transcription, single-stranded RNA can fuse with double-stranded RNA to form R-loops:

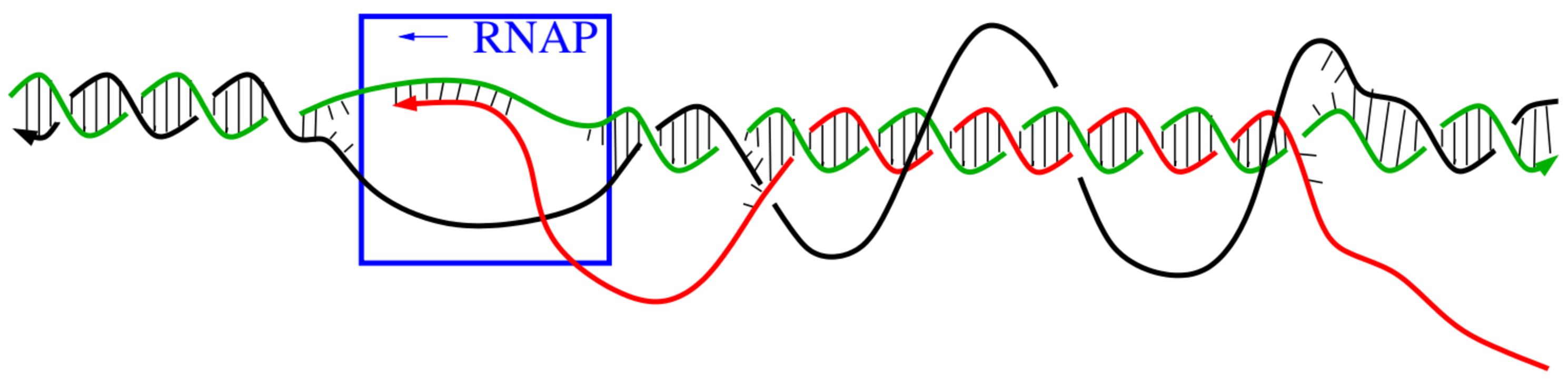Jonoska et al, Using Mathematics to Understand Biological Complexity 2021

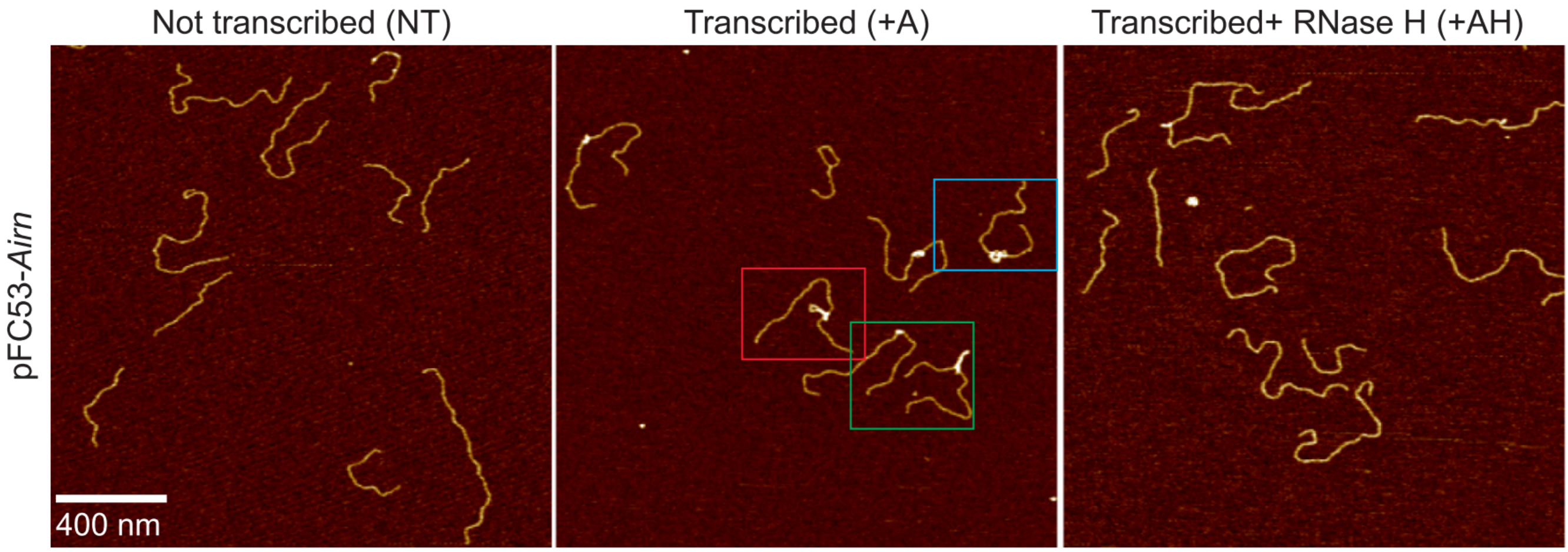Carrasco-Salas et al, Nucleic Acids Res. 2019

The presence of R-loops can affect repair, eg. in human cells.

R-loops

Topologically the DNA:RNA hybrid is a graph with two vertices of degree 3 or 4:

Different parts are single- or double-stranded so may have different stiffness etc.

Knotted theta-graphs

Thetas can also have non-trivial topology -- open questions about minimum number of edges required, etc.

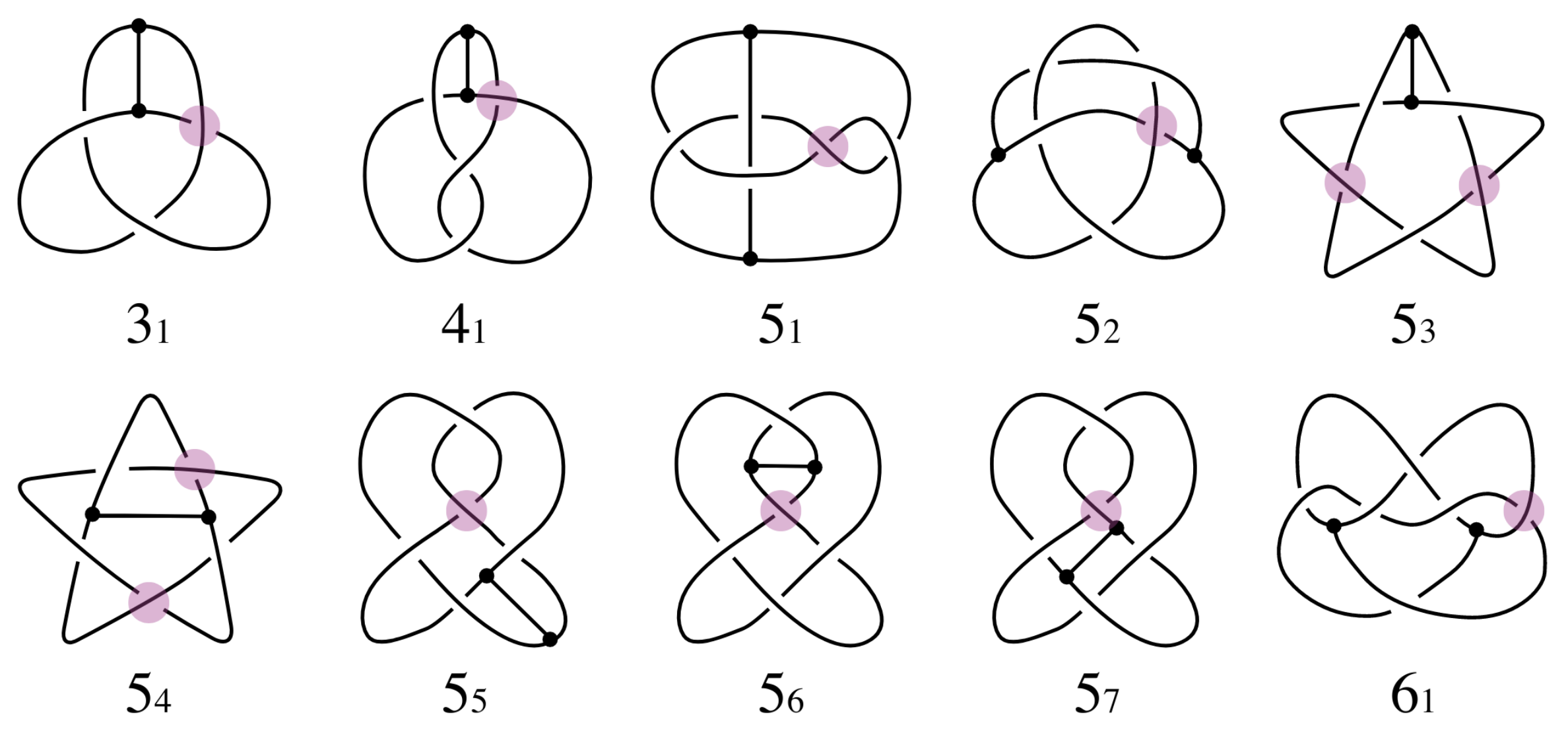Buck & O'Donnol 2018

Monte Carlo methods

BFACF algorithm

The BFACF algorithm (Berg & Foester 1981, Aragão de Carvalho, Caracciolo & Fröhlich 1983 and 1983) is a method for sampling SAWs and SAPs which preserves topology.

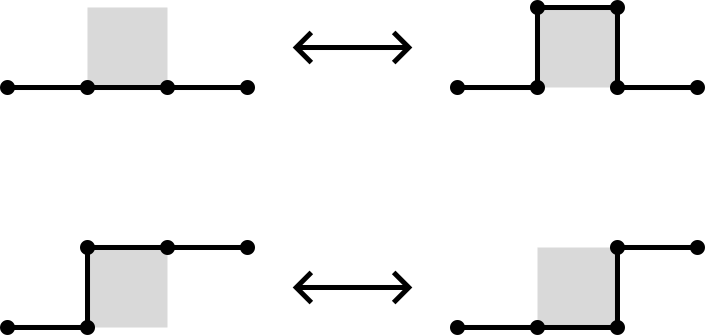
For 2D SAPs it is ergodic while in 3D the ergodicity classes are the knot types. For SAWs the ergodicity classes are walks between two fixed endpoints.

Also works on the triangular lattice.

BFACF algorithm

For the fcc and bcc lattices, Janse van Rensburg and Rechnitzer (2011) found a set of moves which also give the knot types as the ergodicity classes.

BFACF for branched structures

The above BFACF moves can shift vertices of degree 2 and leave vertices of degree 1 fixed.

To accommodate vertices of degree 3, Sokai (2018) found a new set of moves on the square/cubic lattices which can realise any ambient isotopic transformation:

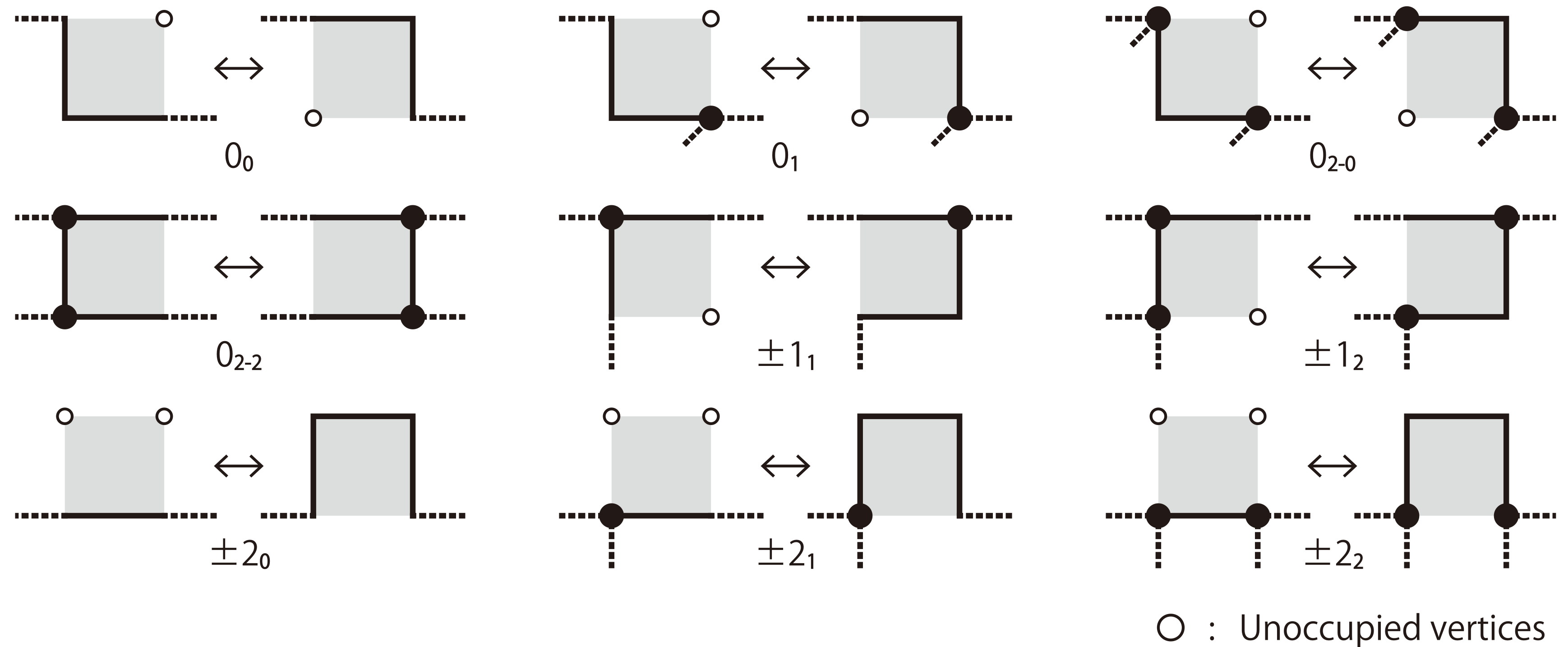
Note that the degree 3 vertices can move around.

BFACF for branched structures

Simpler on the triangular lattice:

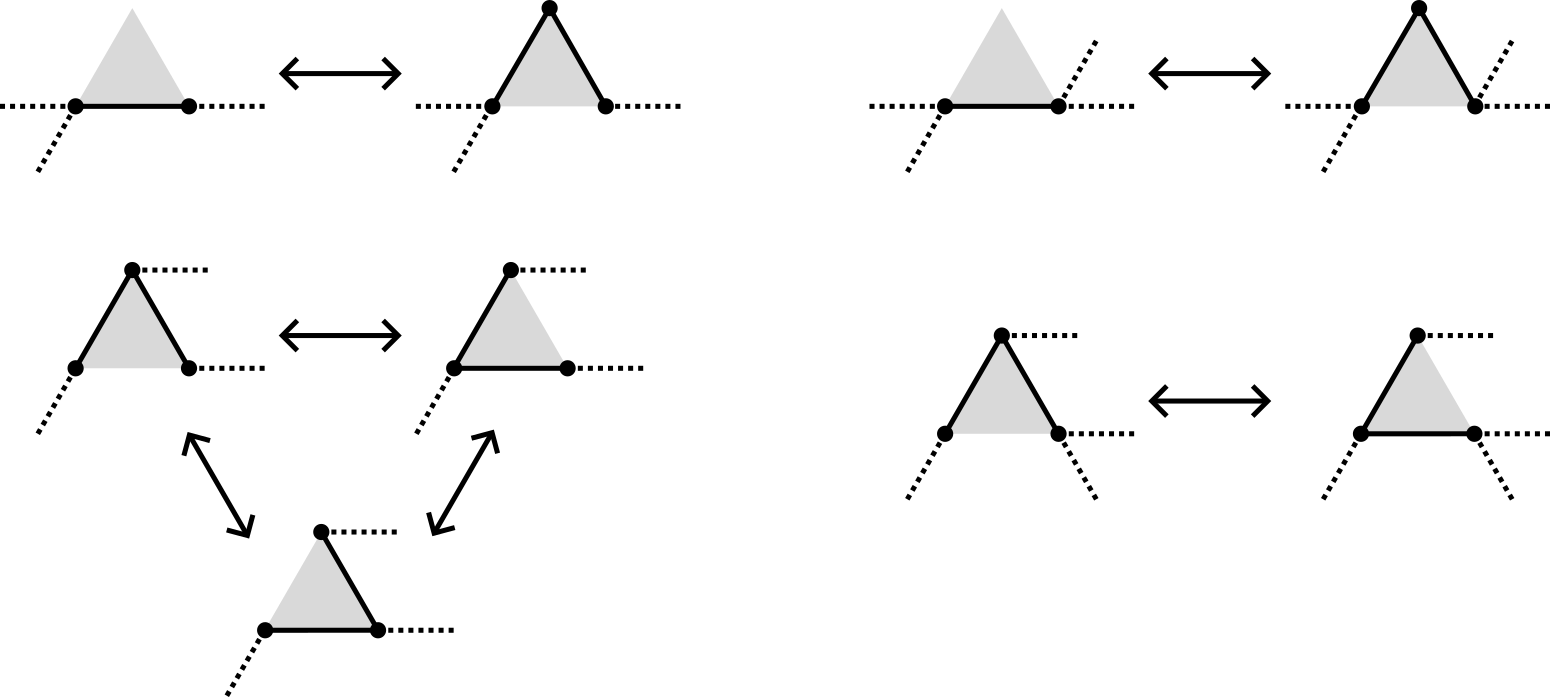
Same moves on the fcc lattice since the faces are still triangles.

Wang-Landau method

We combine the BFACF moves with the Wang-Landau method (2001) to estimate the number $a_n$ of configurations of size $n$.

Start with $f=1$ and arrays $G$ and $H$ both all $0$.

1. For a given configuration $\gamma$, pick a random edge and a random adjacent plaquette. If there is a valid BFACF move, accept with Metropolis probability \[ \mathbb{P}(\gamma \to \gamma') = \min\{1, \exp(G(|\gamma|) - G(|\gamma'|))\},\] else stay in state $\gamma$.
2. Now in state $\gamma''$ (either $\gamma$ or $\gamma'$), increment $G(|\gamma''|)$ by $f$ and $H(|\gamma''|)$ by 1.
3. If $H$ is sufficiently flat, decrease $f$ (e.g. $f \mapsto f/2$), reset $H=0$ and start again. Otherwise continue with the current value of $f$.
4. When $f$ reaches some small threshold, terminate.

If $m$ is the size of the smallest configuration, set $g=G(m)$ and then for each $n$ set \[ A(n) = \exp(G(n) - g)\cdot a_m\cdot m/n. \] Then $A(n) \approx a_n$.

Wang-Landau method

Easily generalises to measure more than just size -- e.g. we will estimate $\theta_{n,k}$, the number of thetas of size $n$ with shortest arm of size $k$.

Many other variations -- e.g. change how $f$ decreases, or tune $G$ and then use those values to estimate some other quantity.

(Preliminary) Results: Thetas

The number of thetas

The number $p_n$ of SAPs on the lattice is $\sim \text{const.} n^g \mu^n$ where (Guttmann 2009) \[ g = \begin{cases} -5/2 & d=2 \\ -2.76279 & d=3 \end{cases} \] and $\mu$ is the connective constant of the lattice (Jensen 2004, Clisby 2022): \begin{align*} \mu_\text{tri} &= 4.150797226(26) \\ \mu_\text{fcc} &= 10.03705785(14) \end{align*}

Expect $\theta_n \sim \text{const.}n^h \mu^n$ for the same $\mu$.

The number of thetas

Estimating the exponent $h$ for the triangular lattice (10 independent runs, $N=500$):

$h \approx g+1$ $\leftrightarrow$ $O(n)$ places to position a small loop within a big polygon.

The number of thetas

Estimating the exponent $h$ for the fcc lattice (10 independent runs, $N=300$):

Again $h \approx g+1$.

Note that these thetas are unknotted so should really use $\mu_0$ but don't have an estimate for that.

Mean length of shortest theta arm

If $\sigma(\theta)$ is the length of the shortest arm then expect (?) $\langle \sigma \rangle_n \sim \text{const.}n^s$ for some $s$. Estimating $s$ for the triangular lattice (10 independent runs, $N=500$):

Mean length of shortest theta arm

Estimating $s$ for the fcc lattice (10 independent runs, $N=300$):

Still some curvature $\rightarrow$ $s \approx 0.75$ is very plausible.

Mean length of two shortest theta arms

Can also look at $\tau(\theta)$, the sum of the two shortest arms. Triangular lattice (10 independent runs, $N=400$):

Likely the same exponent as for shortest arm.

Mean length of two shortest theta arms

fcc lattice (10 independent runs, $N=300$):

Likely the same exponent, more data may help.

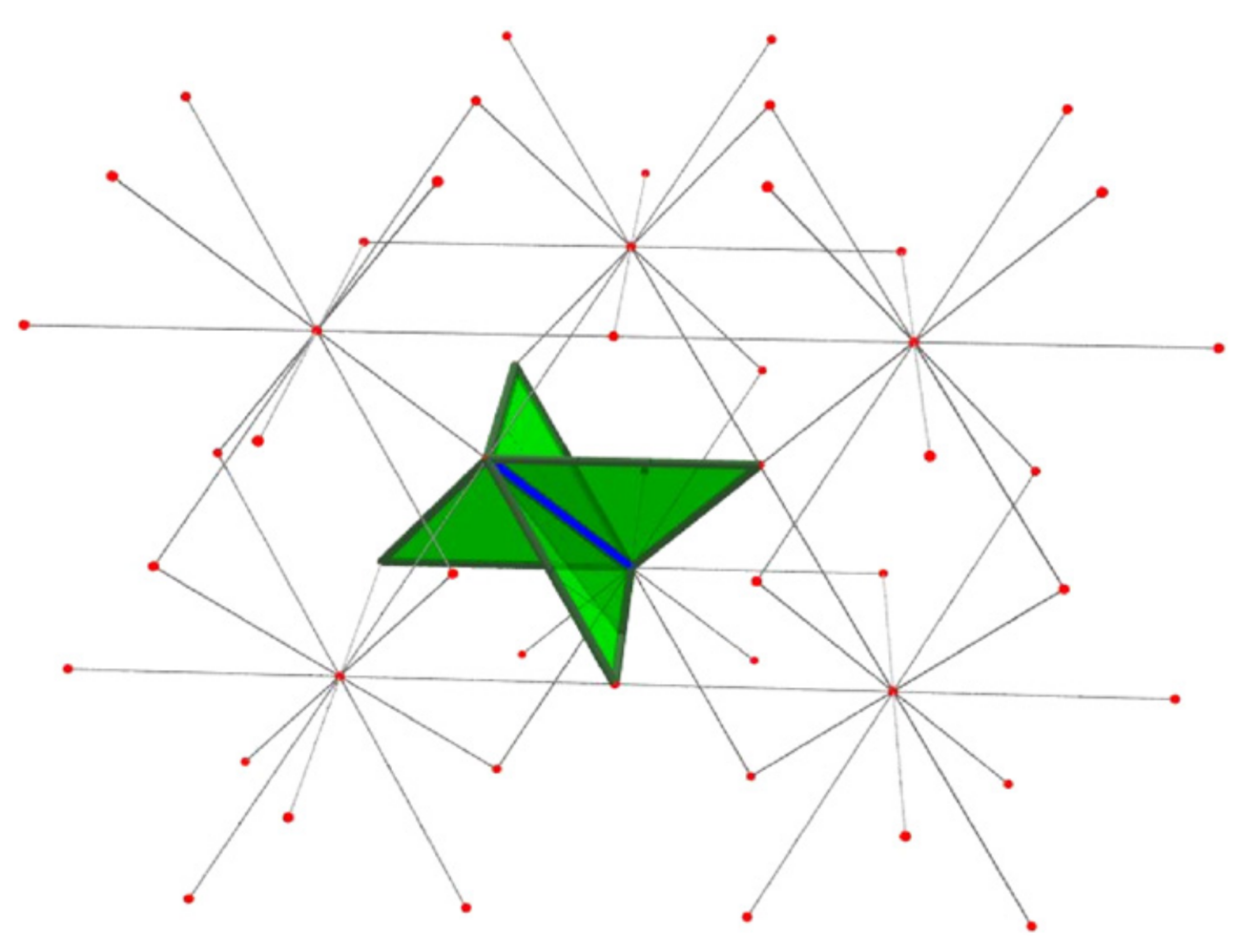
Samples

$N=200$

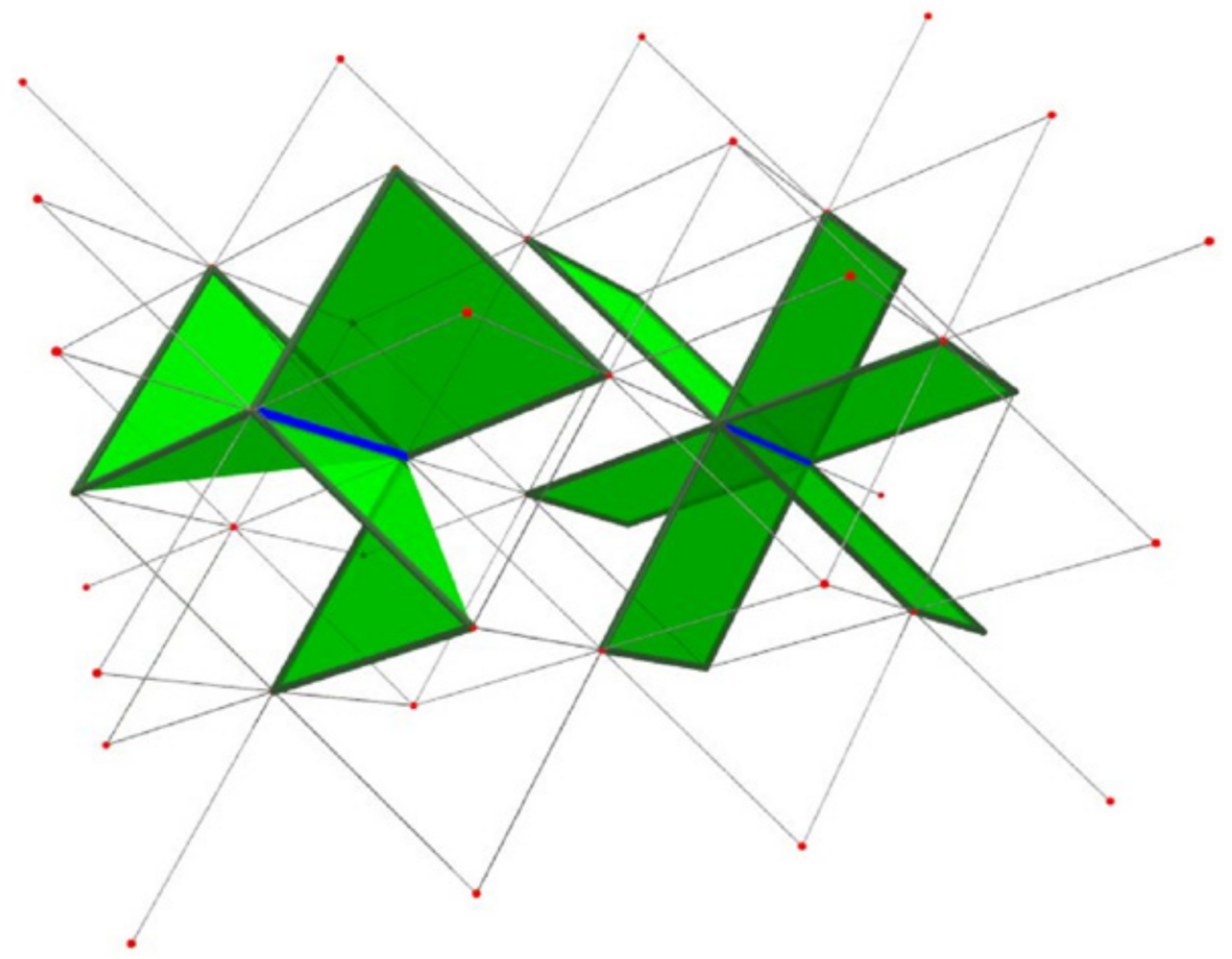
Samples

$N=120$

(Preliminary) results: tadpoles

The number of tadpoles

The number $c_n$ of SAWs on the lattice is $\sim \text{const.} n^{\gamma-1}\mu^n$ where (Clisby 2017) \[ \gamma = \begin{cases} 43/32 & d=2 \\ 1.15695300(95) & d=3 \end{cases} \]

Expect $t_n \sim \text{const.}n^r \mu^n$ for some $r$.

The number of tadpoles

Estimating $r$ for the triangular lattice (10 independent samples, $N=300$):

Note that $\gamma-1 = 11/32 = 0.34375$.

The number of tadpoles

Estimating $r$ for the fcc lattice (10 independent runs, $N=200$):

Note that $\gamma-1 = 0.156953$.

Mean size of tadpole head

Let $\eta(\varphi)$ be the number of edges in the "head" of a tadpole $\varphi$. How does $\langle \eta \rangle_n$ scale? Still a power law? Triangular lattice (10 independent samples, $N=300$)

Small exponent and still some curvature... not so convincing.

Mean size of tadpole head

Try for $\log$ instead of power law:

More convincing (?)

Mean size of tadpole head

Repeating for fcc lattices (10 independent runs, $N=200$), trying a power law:

Mean size of tadpole head

Trying log scaling:

Inverted tadpoles

In 2D there are two different topologies for tadpoles: "regular" and "inverted"

All the previous data was for regular tadpoles.

Let $i_n$ be the number of inverted tadpoles.

Expect different behaviour -- regular tadpoles are long SAWs with a little loop, but with inverted there is competition between the size of the head and tail?

The number of inverted tadpoles

Harder to sample -- configurations at either extreme of head/tail size are very rare. Estimating exponent for triangular lattice (10 independent runs, $N=100$):

Mean size of inverted tadpole head/tail

Seems that both head and tail scale as $O(n)$ (10 independent runs, $N=100$):

Samples

$N=150$

Samples

$N=100$

Samples

$N=50$

Future work

• More data! Square and cubic lattices too
• Other shapes?
• How do knots affect things?
• Minimum sizes of prime theta knots
• Introduce weights to model R-loops
• Improve the algorithm (GAS? pivots?)